Kinematics primitives

The dv-processing library provides a minimal implementation of kinematic transformation primitives that are useful for geometric computer vision algorithms. This includes transformations of 3D points using transformation matrices and handling rigid-body motion trajectories over time. These basic primitives can be used to implement motion compensation algorithm for event data, which can be used to reduce or eliminate motion blur in the event stream. The underlying implementation uses mathematical operations from Eigen library, so the mathematical operations are expected to be highly efficient.

Transformation

A transformation in dv-processing describes an object’s orientation and position in 3D space at a certain point in time. Transformation contains a timestamp, rotational and translational transformation expressed as a 4x4 homogenous transformation matrix T, like this:

Here:

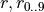• - is a rotation matrix (and it’s coefficients) that describes an object’s rotation.

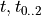• - is a vector describing translational vector, which is an object’s displacement.

A transformation matrix together with a timestamp describes complete attitude with 6 degrees of freedom. This transformation can be applied to other transformations as well as 3D points to obtain a new relative position with the applied transformation. The transformation is implemented in the dv::kinematics::Transformation class, which is a templated class. The template parameter sets the underlying matrix scalar data type for the 4x4 matrix, which is either float or double. To simplify the use case, two predefined aliases are defined: dv::kinematics::Transformationf and dv::kinematics::Transformationd - they differ in the underlying scalar data type:

• Transformationf uses 32-bit single precision floating point values,

• Transformationd uses 64-bit double precision floating point values.

The library usually prefers the use of single precision floating point scalar type, since the representation is accurate enough for sub-millimeter accuracy with lower memory footprint.

The following sample code shows how to initialize a transformation and apply it to a 3D point.

C++Python

#include <dv-processing/kinematics/transformation.hpp>

#include <iostream>

int main() {
    Eigen::Matrix4f matrix;

    // Mirror rotation matrix with 0.5 translational offsets on all axes. The rotation matrix should flip
    // x and z axes of the input.
    matrix << -1.f, 0.f, 0.f, 0.5f, 0.f, 1.f, 0.f, 0.5f, 0.f, 0.f, -1.f, 0.5f, 0.f, 0.f, 0.f, 1.f;

    // Initialize the transformation with the above matrix. The timestamp can be ignored for this sample, so its set
    // to zero.
    const dv::kinematics::Transformationf transformation(0, matrix);

    // Let's take a sample point with offsets of 1 on all axes.
    const Eigen::Vector3f point(1.f, 1.f, 1.f);

    // Apply this transformation to the above point. This should invert x and z axes and add 0.5 to all values.
    const Eigen::Vector3f transformed = transformation.transformPoint(point);

    // Print the resulting output.
    std::cout << "Transformed from [" << point.transpose() << "] to [" << transformed.transpose() << "]" << std::endl;

    return 0;
}

Linear transformer

A set of transformations that are monotonically increasing in time can be formed into a motion trajectory. Linear transformer can be used to store a set of transformation representing a single objects trajectory and extract transformations at specified points in time, which are calculated using linear interpolation between the nearest available transformations.

The following sample code shows how to use the dv::kinematics::LinearTransformerf class to interpolate intermediate transformations in time:

C++Python

#include <dv-processing/kinematics/linear_transformer.hpp>
#include <dv-processing/kinematics/transformation.hpp>

#include <iostream>

int main() {
    // Declare linear transformer with capacity of 100 transformations. Internally it uses a bounded FIFO queue
    // to manage the transformations.
    dv::kinematics::LinearTransformerf transformer(100);

    // Push first transformation which is an identity matrix, so it starts with no rotation at zero coordinates
    transformer.pushTransformation(
        dv::kinematics::Transformationf(1000000, Eigen::Vector3f(0.f, 0.f, 0.f), Eigen::Quaternionf::Identity()));

    // Add a second transformation with no rotation as well, but with different translational coordinates
    transformer.pushTransformation(
        dv::kinematics::Transformationf(2000000, Eigen::Vector3f(1.f, 2.f, 3.f), Eigen::Quaternionf::Identity()));

    // Interpolate transformation at a midpoint (time-wise), this should device the translational coordinates
    // by a factor of 2.0
    const auto midpoint = transformer.getTransformAt(1500000);

    // Print the resulting output.
    std::cout << "Interpolated position at [" << midpoint->getTimestamp() << "]: ["
              << midpoint->getTranslation().transpose() << "]" << std::endl;

    return 0;
}